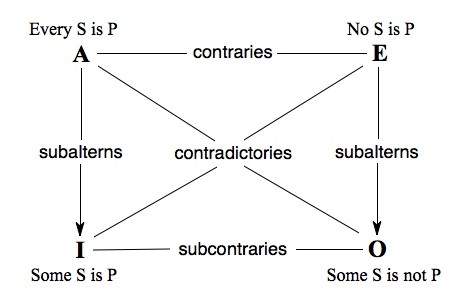
The “square of opposition” is a nifty way to see several logical relationships between four types of propositions. Substitute something in for S (subject) and P (predicate) and you can see how this works.
Let’s use “Evangelical” for “S” and “Republican” for P.
There are four possible relationships.
Two universal propositions:
- A: All Evangelicals are Republicans (universal affirmative)
- E: No Evangelicals are Republicans (universal negative)
And two particular propositions:
- I: Some Evangelicals are Republicans (particular affirmative)
- O: Some Evangelicals are not Republicans (particular negative)
There are multiple observations that can be made, but here are a just couple of practical implications.
1. If you want to refute a claim, identify what kind of thing is being proposed. In a sense, the stronger the claim the easier the potential refutation. For example, if someone affirms a universal (A or E), one only needs to find a single example to count as a “contradiction” (follow the diagonal line). In other words, if I claim A (All Evangelicals are Republicans) you only need to provide one counter-example of an Evangelical Democrat to demonstrate O (Some Evangelicals are not Republicans). Similarly, in responding to E (No Evangelicals are Republicans) you only need to find one Republican Evangelical to demonstrate the contradictory I (Some Evangelicals are Republicans).
2. In making a claim, avoid universal claims unless there can be no possible exception. Make a claim that you can defend.
A couple of years ago at the breakfast table my 4-year-old son and 6-year-old daughter provided a nice example of the square of opposition in action:
4-year-old: I know everything.
6-year-old: No, you don’t.
4-year-old: Yes, I do!
6-year-old: Ok . . . then what do cheetahs eat?
4-year-old: (Long pause.)
6-year-old: See, you don’t know everything!
Score one for the 6-year-old. She took his propositional claim (“I know everything”) and intuitively recognized that in order to refute it, she did not need to prove the contrary claim (i.e., “You know nothing”) but only had to show a contradiction with his proposal (i.e., “There’s at least one thing you don’t know”).
And of course if he had given the right answer—they eat eat gazelles, impala, deer, and also rabbits, frogs, birds, lizards, eggs, and watermelon—that still wouldn’t have proven his claim. She would just need to figure out another contradiction.


















